مدير منتديات الهندسة
مدير المنتديات
عدد المساهمات : 137
نقاط : 346
السٌّمعَة : 2
تاريخ التسجيل : 31/10/2010
 |  موضوع: Produit vectoriel ( cours ) 1ère Anné ST  الجمعة يناير 28, 2011 3:06 pm | |
| Définition : soit E
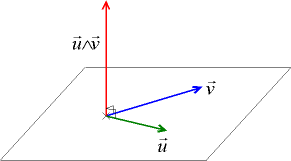
Soit E un espace vectoriel euclidien orienté de dimension 3. Par le choix d'une base orthonormée, E peut être identifié avec l'espace R3, mais cette identification n'est pas obligatoire pour définir le produit vectoriel.
D'un point de vue géométrique, le produit vectoriel de deux vecteurs  et  de E non colinéaires se définit comme l'unique vecteur  tel que :
En particulier :
- deux vecteurs sont colinéaires si et seulement si leur produit vectoriel est nul ;
- deux vecteurs sont orthogonaux si et seulement si la norme de leur produit vectoriel est égale au produit de leurs normes.
La notion d'orientation peut ici être comprise de manière élémentaire en utilisant la règle de la main droite : le pouce, l'index et le majeur écartés en un trièdre indiquent respectivement le sens de u, de v et de w. Cette définition, utilisée dans l'enseignement secondaire, n'est pas totalement satisfaisante.
Définition par le produit mixte[modifier]
Une seconde définition utilise la théorie des déterminants et la notion de produit mixte comme point de départ. Le produit mixte de trois vecteurs u,v,w, noté [u,v,w], est le déterminant de ces trois vecteurs dans une base orthonormale
directe quelconque. La formule de changement de base montre que ce
déterminant est indépendant du choix de la base ; géométriquement il
est égal au volume orienté du parallélépipède appuyé sur les vecteurs u,v,w. Le produit vectoriel de deux vecteurs u et v est l'unique vecteur  tel que, pour tout w, on a :
 . L'existence et l'unicité d'un tel vecteur sont un cas particulier simple du théorème de représentation de Riesz. Le produit vectoriel s'interprète comme les variations du volume orienté d'un parallélépipède en fonction du troisième côté.
Avec une telle définition, il est possible de définir, dans un espace vectoriel orienté de dimension n + 1, le produit vectoriel de n vecteurs.
[Dérouler] Équivalence des deux premières définitions
Prenons la seconde définition ; et appliquons l'identité ci-dessus à w= u et v respectivement. On obtient :  et  . Donc, le vecteur  est orthogonal à u et à v. De plus, si u,v,w forme une base directe, le produit mixte [u,v,w] est strictement positif. De fait, et w ne sont pas séparés par le plan vectoriel engendré par u et v. Autrement dit, u, v, u v forme une base directe. Si w est de plus unitaire (de norme 1), alors  n'est autre que la norme euclidienne de u v. Cette dernière est donc le produit mixte [u,v,w] ; soit le volume orienté du parallélipipède appuyé sur u, v et w. Ce volume est le produit de la hauteur  par l'aire de la base  . De suite :  .
Calcul en composantes[modifier]
Le choix d'une base orthonormée directe donne une identification de E et de ℝ3. Notons les coordonnées u=(u1, u2, u3) et v=(v1, v2, v3). Leur produit vectoriel est donné par :
Cette identité pourrait être prise comme une troisième définition, à
condition de prouver que le vecteur obtenu est indépendant de la base
orthonormale directe choisie pour le calculer.
[Dérouler] Calculs
Introduisons un vecteur w= (w1,w2,w3) et utilisons la définition par le produit mixte. Ce dernier est donné par :
 En développant le déterminant par rapport à la troisième colonne :
 | إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
 . Ce qui donne les coefficients de .
Propriétés[modifier]
Propriétés algébriques[modifier]
Le produit vectoriel est un produit distributif, anticommutatif, non associatif :
Ces
propriétés découlent immédiatement de la définition du produit
vectoriel par le produit mixte et des propriétés algébriques du
déterminant.
Le produit vectoriel satisfait l'identité de Jacobi, ce qui en fait un crochet de Lie :
 D'autre part, il satisfait aux identités de Lagrange (égalités du double produit vectoriel) :
 [10]  [Dérouler] Démonstration
Soient 
On construit une base orthonormée  directe de  : On pose 
Ensuite on choisit  comme étant l'unique vecteur directement orthogonal à  dans le plan définit par  .
Enfin on pose  tel que 
Dans cette base, les vecteurs  ont pour coordonnées :
   avec a,b,c,d,e,f réels.
Ainsi :
| إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
   De même : | إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
D'où l'égalité.
En partant de l'identité algébrique :
| إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
 , on peut démontrer facilement l'égalité (Identité de Lagrange) :
 que l'on peut aussi écrire sous la forme :
 ce qui équivaut à l'identité trigonométrique :
 , et qui n'est rien d'autre qu'une des façons d'écrire le théorème de Pythagore.
Invariance par isométries[modifier]
Le produit vectoriel est invariant par l'action des isométries vectorielles directes. Plus exactement, pour tous vecteurs u et v de E et pour toute rotation f de E, on a :
 . Cette identité peut être prouvée différemment suivant l'approche adoptée :
Définition géométrique : L'identité est immédiate avec la première définition, car f préserve l'orthogonalité, l'orientation et les longueurs.
Produit mixte : L'isomorphisme linéaire f laisse invariant le produit mixte de trois vecteurs. En effet, le produit mixte de f(u), f(v), f(w) peut être calculé dans l'image par f de la base orthonormée directe dans la quelle le produit mixte de u, v et w est calculé. De fait, l'identité précédente s'obtient immédiatement :
| إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
 . Définitions alternatives[modifier]
Comme produit de Lie[modifier]
Toute isométrie directe de R3 est une rotation vectorielle. L'ensemble des isométries directes forme un groupe de Lie classique noté SO(3) (autrement dit, un sous-groupe fermé de GL3(R)). Son algèbre de Lie, notée so(3) est la sous-algèbre de Lie de gl3(R) définie comme l'espace tangent de SO(3) en l'identité. Un calcul direct montre qu'il est l'espace des matrices antisymétriques de taille 3. Cet espace est a fortiori stable par le crochet de Lie.
Toute matrice antisymétrique M de taille 3 s'écrit de manière unique :
 . En identifiant M et le vecteur (a, b, c), on définit un isomorphisme linéaire entre so(3) et R3. Le crochet de Lie se transporte via cet isomorphisme, et R3 hérite d'une structure d'algèbre de Lie. Le crochet [u, v] de deux vecteurs est précisément le produit vectoriel de u et de v.
En effet, si u1=(a1, b1, c1), et u2=(a2, b2, c2), leur crochet se
calcule en introduisant les matrices antisymétriques correspondantes M1 et M2 :
| إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
Le vecteur correspondant, à savoir [u1,u2], a donc pour coordonnées
(b1c2-b2c1, a2c1-a1c2, a1b2-a2b1). Cette approche redéfinit donc le
produit vectoriel.
Si on suit cette approche, il est possible de prouver directement l'invariance du produit vectoriel par isométries
. En tant qu'algèbres de Lie, so(3) a été identifié à R3. L'action (linéaire) de SO3(R) sur R3 s'identifie à l'action par conjugaison sur so(3). SO3(R) opère donc par automorphisme d'algèbres de Lie. Autrement dit, l'identité ci-dessus est vérifiée.
Comme produit de quaternions imaginaires[modifier]
Il est possible de retrouver produit vectoriel et produit scalaire à partir du produit de deux quaternions purs. Pour rappel, le corps (non commutatif) des quaternions H est l'unique extension de R de dimension 4. Sa base canonique est (1, i, j, k) où le sous-espace engendré par i, j, k forme l'espace des quaternions purs, canoniquement identifié avec R3. Ces éléments vérifient :
 ; | إضغط هنا لرؤية الصورة بحجمها الطبيعي. |
 . Si q1=a1i+b1j+c1k et q2 = a2i+b2j+c2k, le produit q1q2 se calcule immédiatement :
q1q2 = − (a1a2 + b1b2 + c1c2) + (b1c2 − b2c1)i + (c1a2 − c2a1)j + (a1b2 − a2b1)k. La partie réelle est au signe près le produit scalaire de q1 et de q2, la partie imaginaire est un quaternion pur qui correspond au produit vectoriel, après identification avec R3.
Cette coïncidence trouve ses explications dans le paramétrage du groupe SO(3) par les quaternions unitaires.
[Dérouler] Éléments d'explication
L'application linéaire envoyant 1 sur 1, i sur -i, j sur -j et k sur -k est appelée la conjugaison. Le conjugué d'un quaternion q est noté  . Un quaternion est un réel si et seulement s'il est égal à son conjugué. L'application  définit un produit scalaire sur l'espace vectoriel H. Un quaternion est dit unitaire lorsqu'il est de norme
1. Dans ce cas, il suit de la définition même du produit scalaire qu'il
est inversible et que son inverse est son conjugué. L'ensemble des
quaternions unitaires, la sphère unité S3, forme un groupe (de Lie) compact et simplement connexe. Il agit sur l'espace des quaternions imaginaires par conjugaison. Pour tout quaternion unitaire u et pour tout quaternion imaginaire q :
 . Cette action préserve la norme ; autrement dit, c'est une action par isométries. Elle définit donc un morphisme de groupes :
 Ce morphisme est en réalité le revêtement universel du groupe SO(3). Il induit donc un isomorphisme entre les algèbres de Lie.
L'algèbre de Lie de S3
est justement l'espace des quaternions imaginaires munis du crochet de
Lie obtenu comme la partie imaginaire du produit des quaternions. Cette
algèbre de Lie est isomorphe à l'algèbre de Lie R3 (muni du produit vectoriel).
C'est la raison fondamentale pour laquelle la partie imaginaire de deux
quaternions imaginaires s'identifie au produit vectoriel.
Il est de nouveau possible de justifier l'invariance par
isométrie. Toute isométrie de l'espace des quaternions imaginaires
s'écrit comme la conjugaison par un quaternion unitaire. Si q est un quaternion unitaire, et q1, q2 sont des quaternions imaginaires, il suffit de constater :
 pour en déduire l'invariance par isométrie du produit vectoriel
| |
|
اليومية
est de 
.
,
,
