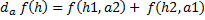Cours.

1. Définition du Produit vectoriel dans E espace euclidien de dimension 3.
   
2. Propriétés.
   
3. Produit mixte. (Généralisable dans un ev de dimension n).
   
4. Généralisation du produit vectoriel.
   
5. Propriétés différentielles et de continuité.
   

---

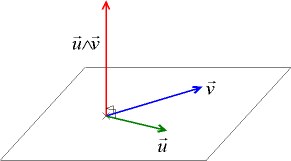
1°) Définition du Produit vectoriel dans E espace euclidien de dimension 3.


Dans une base orthonormée

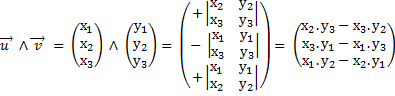
Remarque : Notez la permutation circulaire permettant de passer d'une ligne à l'autre !

Haut de page
2°) Propriétés.

• L’application produit vectoriel est bilinéaire et antisymétrique (u
  &
  
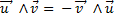• La famille (u,v) est liée
  
  ⇔
  
• 
  

• 
  
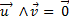
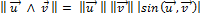
• L’aire du parallélogramme construit sur u et vest égale à :
  
  
  
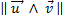
• Double produit vectoriel : (attention, il faut que les coordonnées des vecteurs commutent !)
  
  
  
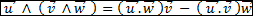
• Identité de Jacobi : du mathématicien allemand JACOBI Carl Gustav Jacob (1804-1851)
  
  
  

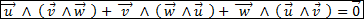
Haut de page
3°) Produit mixte. (Généralisable dans un ev de dimension n)


<blockquote>

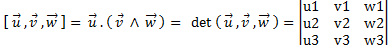
L’application produit mixte est antisymétrique et trilinéaire.


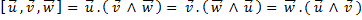
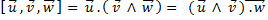Théorème de Hadamard :



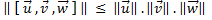
Avec égalité si l’un des vecteurs est nul ou si (u,v,w ) est une BON .
</blockquote>
4°) Généralisation du produit vectoriel. [Ladeg p 125]


<blockquote>
Pour
tout couple de vecteurs (u,v) de l’espace vectoriel euclidien orienté
de dimension 3, Il existe un unique vecteur V tel que pour tout vecteur
w , on a :

.
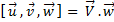
Ce vecteur V est appelé produit vectoriel de u et v.
Remarque : Cette définition est généralisable en dimension n pour n-1 vecteur (n>2)
</blockquote>

Haut de page
5°) Propriétés différentielles et de continuité.



5.a : Continuité des applications multilinéaires en dimension finie.

Théorème. [Monier2p68]
Soit pour k entier, Ek et F des IK-ev.
Si les Ek sont de dimensions finies, alors toute application multilinéaire de ∏Ek dans F est continue.
Conséquences : Pour E de dimension finie.
Pour y fixé, l’application de E → IK qui : x → < x , y > est continue (car linéaire).
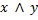
Pour y fixé, l’application de E → E qui : x → est continue (car lineaire).
Les applications normes, produit scalaire, produit mixte et produit vectoriel sont continues.
5.b : Dérivée et différentielle.

Fonctions bilinéaires : [SoroAn]p354
f bilinéaire de IRp × IRn dans F ⇒ f est différentiable et

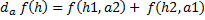Conséquences
Le produit scalaire et le produit vectoriel sont différentiables et :